
Welcome to Hilliard City Schools Elementary Parent Math Support Page. Helping to support your child’s development in math is crucial to their success in school and in life. There are many simple and fun things you can do as a family to help your child to be successful, and we are here to help along the way!
We’ve developed this page to…
- answer common questions,
- spread ideas, and
- give you resources that may help at home.
As always, you and your child’s teacher know your child best, so feel free to always reach out to them with any further questions you may have regarding your child.
What strategies might my child be learning for addition/subtraction?
In preschool and kindergarten, children focus on exploring number relationships that involve counting. For example, if we add one more to a group of four, we have five (because we can count four then five. These counting strategies can be connected to addition and subtraction since we can count up by one or two for addition (or back by one or two for subtraction). Subitizing is another skill that students practice by looking at a group of dots and “seeing” them in different ways. For example, we might see five as two dots and three dots while someone else sees one dot and four dots. Which addition and subtraction facts do you think of when you see these dot patterns?

Often children begin by modeling or using objects (such as blocks) to explore this concept before moving to draw pictures. It is important to help children make the connection between these objects and pictures with the symbols we use to represent the equation.
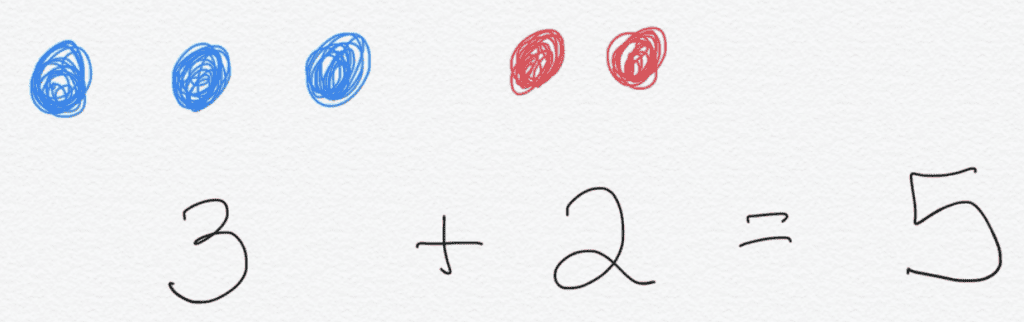 Rather than wait to introduce subtraction after all of the addition facts are introduced, we introduce these facts together. It is powerful for children to notice the relationship between fact families. For example, knowing 2 + 3 = 5 might help a child determine that 5 – 3 = 2. Research (Baroody & Rosu, 2004, Siegler, 1995) supports that when students “invent, use, share, and explain different strategies”, they learn their basic math facts better. In fact, the number of strategies that students use is a predictor of their later learning. This means that the more strategies they are able to understand and use, the more “tools” they have available in their toolbox. While this might seem inefficient in the early grades, these different strategies are an essential part of building number sense and fluency.
Rather than wait to introduce subtraction after all of the addition facts are introduced, we introduce these facts together. It is powerful for children to notice the relationship between fact families. For example, knowing 2 + 3 = 5 might help a child determine that 5 – 3 = 2. Research (Baroody & Rosu, 2004, Siegler, 1995) supports that when students “invent, use, share, and explain different strategies”, they learn their basic math facts better. In fact, the number of strategies that students use is a predictor of their later learning. This means that the more strategies they are able to understand and use, the more “tools” they have available in their toolbox. While this might seem inefficient in the early grades, these different strategies are an essential part of building number sense and fluency.
As students move through kindergarten and into grade 1, the focus changes from using counting strategies to reasoning strategies. These might include:
Doubles Plus One
Counting On
Break Apart To Make A Ten
Partial Sums
Through various classroom activities, children practice these basic facts. As they have the opportunity to use different strategies, they decide which strategies work best with particular number pairs.
As children move into grade 2 and beyond, these same strategies will work with larger numbers. Children begin to notice which methods are more efficient – leading them to use partial sums, partial differences, and the traditional algorithms we learned in school. As children develop fluency with whole numbers, many of these strategies can be transferred to their work with fractions.
What are the Standards for Mathematical Practice? Why are these important?
The Standards for Mathematical Practice (SMPs) include 8 skills/behaviors that educators work to develop in their math learners. The SMPs are the work that the students do in math class, including making sense of problems. Unlike the content standards, that change from grade to grade, the SMPs remain constant across K-12. Any time children are working on or talking about mathematical ideas, they are using the SMPs. Every math lesson will involve the practice standards, but not every lesson will include each one. While some are more easily observed than others, all of these skills are important in developing a well-rounded mathematician.
 “The mathematical practices for each grade, together with Ohio’s Learning Standards for Mathematics, prescribe that students experience mathematics as a rigorous, coherent, useful and logical subject. The mathematical practices represent a picture of what it looks like for students to understand and do mathematics in the classroom and should be integrated into every mathematics lesson for all students” (Ohio Department of Education).
“The mathematical practices for each grade, together with Ohio’s Learning Standards for Mathematics, prescribe that students experience mathematics as a rigorous, coherent, useful and logical subject. The mathematical practices represent a picture of what it looks like for students to understand and do mathematics in the classroom and should be integrated into every mathematics lesson for all students” (Ohio Department of Education).
Parent Guide about the Standards for Mathematical Practice
*This parent guide includes questions you can ask your child to develop those skills.
What are Ohio’s Math Content Standards for Learning for my child’s grade level?
Learning standards are the skills and concepts identified by the state that will prepare students to be ready for their work after high school. While no set of standards is a complete body of knowledge that is needed for students, these standards provide guidance for what children need to know and do at each grade level. Teachers measure the students’ learning and progress with these skills through formative and summative assessments. The state tests that are taken in grades 3-8 each year are also based on these learning standards.
What is math fluency? How can I help my child improve?
Becoming fluent with basic facts is an essential piece of elementary school mathematics. Basic facts are typically defined as the single-digit computation for each operation, such as 2 + 3, 7 – 4, 6 x 2, and 18 ÷ 9. “Knowing” facts allows children to devote mental resources to think about other pieces of their work. Without fluency, students have a hard time learning multidigit calculations. They also face roadblocks in learning multiplication, and division, as well as working with fractions (Davenport, Henry, Clements, & Sarama’s No More Math Fact Frenzy, p. 16).
When we think about fluency, we are focused on flexibility as well as efficiency (speed) and accuracy (correctness). It can be helpful to think about being fluent in a foreign language. If you cannot think of the exact word, you might have the flexibility to describe what you want to say in another way. You would be considered fluent in a language if your message is clear – even without efficient and proper phrasing. In math, a child who has a strategy to figure out a basic fact in a way that is flexible, accurate, and efficient can be considered fluent.
More information about building fluency for specific facts can be found in the sections for strategies for addition/subtraction and multiplication/division.
Fluency goes beyond basic facts and is an essential part of computation. For ideas about how students use these strategies, see these brochures from Howard County.
How can I help my child learn their math facts?
While you might remember flashcards and timed tests as a part of your experience in learning math facts, it is likely that you use derived facts more than you realize. Derived facts are when you use something that is partly known to help you figure out an unknown piece of information. For example, if you are trying to figure out 3 x 8, you might use derived facts to help you find the product is 24.
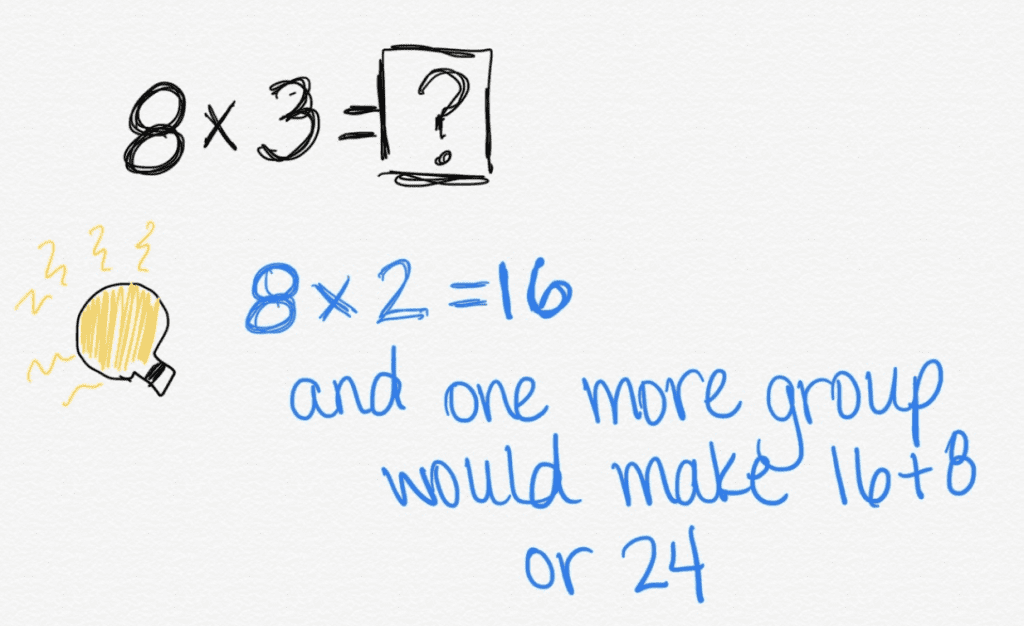 Asking questions of your child and being curious alongside them is a great way to help them learn their math facts. Some questions you might consider as you look at basic facts include:
Asking questions of your child and being curious alongside them is a great way to help them learn their math facts. Some questions you might consider as you look at basic facts include:
- What do you notice?
- Could you tell me a story about these numbers?
- Does this problem remind you of another problem?
- Can you draw a picture to solve the problem?
- What are you trying to find out about this problem?
- Is your answer reasonable? Does it make sense?
Multiply by 3
Multiply by 5
Multiply by 6
Multiply by 7
Multiply by 8
Multiply by 9
Multiply by 10
Games are a fun way to explore and practice basic facts. There are many games available at youcubed.org that you can play with your child. Remember to allow your child to use the strategies that make sense to them. While this might seem time-consuming at first, this is an important step in the learning process. As they have more exposure to the basic facts, they will begin to see connections between related facts and be faster in providing the answer.
Why does today’s math look different than what I learned when I was in school?
Fifty years ago, the job market employed many people whose basic role was to perform calculations. Thinking about the learning we did in our personal elementary school experience, much of the work focused on calculation. In today’s jobs, technology does the calculations. The workforce needs employees who can estimate, reason, and understand relationships about the information they see. Employers are looking for workers who can approach a situation, ask questions, determine necessary information, and think about how they might work toward a solution.
 We also know more about how the brain learns. Visuals are a critical piece of learning mathematics. Research (Boaler, 2016) found that as children abandon counting on their fingers, they continue to “see” these fingers in their minds as they perform calculations. It is important that we not ask children to stop using their fingers before they are ready! Our classrooms have many manipulatives available to help develop this visual imagery, such as:
We also know more about how the brain learns. Visuals are a critical piece of learning mathematics. Research (Boaler, 2016) found that as children abandon counting on their fingers, they continue to “see” these fingers in their minds as they perform calculations. It is important that we not ask children to stop using their fingers before they are ready! Our classrooms have many manipulatives available to help develop this visual imagery, such as:
- Counters
- Ten Frames and Number Frames
- Pattern Blocks
- Base 10 Blocks
- Fraction Circles and Bars
- Cuisenaire Rods
In our classrooms, we use many activities to promote justification and reasoning – as well as build fluency and flexibility with numbers. We emphasize the Standards for Mathematical Practice. These activities might include:
- Three Act Tasks: A story is told in three phases, often through videos. In the first phase, something happens that causes children to notice and wonder. The second phase provides additional information that will help answer the question that is likely to arise from the initial situation. Children devise a plan for using this information to answer their initial question and possible solutions are shared. The third phase provides the solution.
- Which One Doesn’t Belong: Four images are displayed and children choose the one that they believe does not belong in the group. Because there is no “one” correct answer, this is a wonderful way to invite children to share their reasoning and justify their answers to classmates.
- Esti-Mysteries: Children are shown an image and asked to make a guess about the number of objects shown. Clues are revealed and children have the opportunity to revise their estimates as they learn new information about the image.
What if my child doesn’t like math?
The myth that some people are “math people” and others aren’t is a thing of the past. All students can enjoy math and see themselves as mathematicians. Teachers and parents can support a growth mindset towards math by first starting with how we talk to the child during math work or about math. The messages that are given to students can directly impact their performance and they need to know their teachers and parents believe in them.
Ideas to help you when working with your child (Ideas Taken and Adapted from Jo Boaler and Youcubed.org)
|
This is a fixed ability message that seems positive but can be damaging. If they struggle with a math problem later they may think they are not smart. |
| 2. Praise mistakes. | Mistakes are when our brain grows! Scientists have found that when people make a mistake in math synapses spark, and there is an activity in the brain that is absent when people get work correct. What this means is that we want people to make mistakes. In fact, making mistakes in math is the most useful thing we can do. These confusions and mistakes are the most useful moments in math learning! |
| 3. Encourage your child to try challenges and take risks in math so that they make mistakes. | Sometimes children will immediately ask for help on a challenging problem. Ask them to work through it a few minutes on their own first. You can say, I don’t want to take the opportunity for you to struggle and your brain to grow.” This productive struggle is important and a difficult balance. You don’t want them to struggle to the point of giving up, so keep encouraging them as they work. Remind them to try a different way, or to think about a tool that can help them solve, even just rereading the problem aloud can help. |
| 4. Never share personal stories of math dislike or failure. Replace sympathetic messages such as “Don’t worry, math isn’t your thing” with positive messages such as “You can do this, I believe in you, math is all about effort and hard work.” | Even though you may dread math homework time, fake it! Act excited to see what they’ve been working on. In an important study, researchers found that when mothers told their daughters they were not good at math in school, their daughter’s achievement declined almost immediately (Eccles & Jacobs, 1986). |
What are some ideas to help my child with word problems?
Students will be introduced to a variety of math word problems starting as early as kindergarten. There are many different ways to pose addition, subtraction, multiplication and division problems. They can be 1 step problems or multiple steps.
The question children are asked to solve can differ. Sometimes they are asked for a result – but other times they are asked to find the change or start of a situation. Here are two examples of problems that use the same numbers and context but ask different questions:
| 8 cars were in the parking lot. 2 drove away. How many cars are now in the parking lot? | Some cars were in the parking lot and 2 drove away. Now there are 6. How many cars were in the parking before? |
There can be several reasons why your child may struggle with problem-solving, but hopefully, these suggestions will help ease your worry and raise your child’s confidence in solving word problems. One very common reason why students struggle is they have difficulty understanding the problem.
Reread
Read the problem a couple of times and think about what is being asked. Ask yourself, what information from the problem do I know?
Visualize
When reading a book students need to understand what they are reading and to do that we tell students to make a movie in their mind as they read. We ask students to the same thing when solving word problems. This is called visualization. We want students to visualize rather than look for keywords to help them. Ask your child to provide evidence for what they see in their mind either by acting it out, using manipulatives, and/or drawing a picture.
Take the Numbers Out
Does your child tend to just pull the numbers from the problem and don’t stop and think about what’s being asked? You can remove the numbers and just discuss what is happening in the problem before you attempt to solve it with numbers. This can remove the distractors and take away some anxiety if they are more worried about getting the answer than really understanding the problem.
Act It Out
Let’s say a problem is telling you that someone shares candy. Act out the problem with candy or using a manipulative to represent the candy. This will help students who have trouble making that picture in their mind. After acting it out ask your child to then draw a picture of what they did.
What questions can I ask my child to support their math thinking?
Clarify Thinking –
- Tell me about that…
- Can you model that using a picture or other math tool?
- Are you saying… (repeat some or all of what the child said and have them verify if correct.)
- What does ___________ mean? (could have them explain their drawing or solution in words)
Explain a Process –
- How will you solve this problem?
- What steps did you use?
- How do you…?
Justify –
- Can you explain what you did and why you did it?
- How might you prove that your answer is correct?
- Why did you do it that way?
- Why did you choose that tool?
- Is that always true? Can you use representations to prove it?
- But what if…?
Reflect-
- How did you figure that out?
- Did you get stuck at any point? If so, how did you get unstuck?
- What was difficult?
- Has your thinking changed?
Need specific ST Math questions that can guide your student through a challenging puzzle? Check out the ST MATH questions Parent Handout
What strategies might my child be learning for multiplication/division?
Many times, children apply what they know about addition and subtraction to help them begin to learn their basic facts for multiplication and division. In beginning to think about multiplication and division, children often consider “fairness”. This reasoning helps them develop the idea of equal groups and sharing. Often children begin by modeling or using objects (such as blocks) to explore this concept before moving to draw pictures. It is important to help children make the connection between these objects and pictures with the symbols we use to represent the equation. When they are able to visualize the quantities, children begin to notice patterns and a structure to mathematics. For example, 3 groups of 4 are the same as doubling 3 groups of 2:
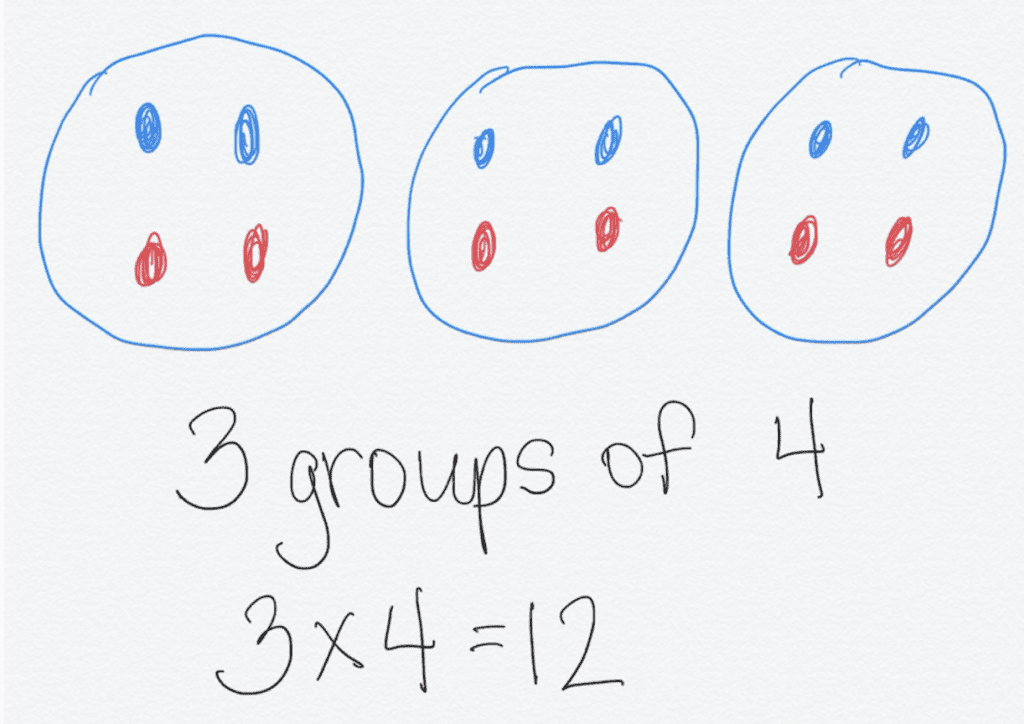
Rather than wait to introduce division after all of the multiplication facts are introduced, we introduce these facts together. It is powerful for children to notice the relationship between fact families. For example, knowing 2 x 5 = 10 might help a child determine that 10 ÷ 5 = 2. Children frequently use skip counting in the beginning stages (such as 3, 6, 9, etc.) and then transition to using more sophisticated strategies. These strategies typically involve recognizing patterns, such as:
- Doubling twice gives the same result as multiplying by 4.
- Multiplying a number by 5 and multiplying the same number by 2, then adding the products gives the same result as multiplying by 7.
Multiply by 3
Multiply by 5
Multiply by 6
Multiply by 7
Multiply by 8
Multiply by 9
Multiply by 10
Partial Products
Partial Quotients
Ohio’s Learning Standards in Mathematics set the expectation that children will be introduced to and then become fluent with their basic multiplication and division facts in grade 3. We recognize that developing this deep understanding of the relationships between these numbers might require more time. Teachers in grade 4 continue to provide opportunities for children to practice their basic facts through games and other activities.
Grade 4 also introduces multi-digit multiplication, such as 23 x 45. The strategies children use to break apart the numbers might appear more time-consuming than the “traditional” way that we learned. The focus of our instruction is on making sense of the magnitude of the numbers and what happens when we multiply.
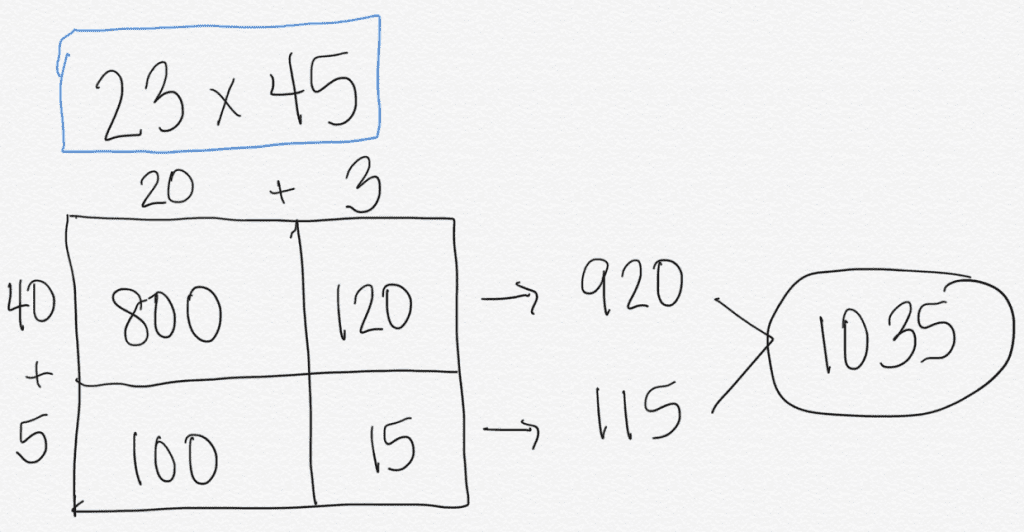 These strategies, such as partial products shown above, can be used in high school when multiplying polynomials. Here is an example of how the same strategy might be used to solve (2x^2 + 3x – 5)(4x + 6).
These strategies, such as partial products shown above, can be used in high school when multiplying polynomials. Here is an example of how the same strategy might be used to solve (2x^2 + 3x – 5)(4x + 6).
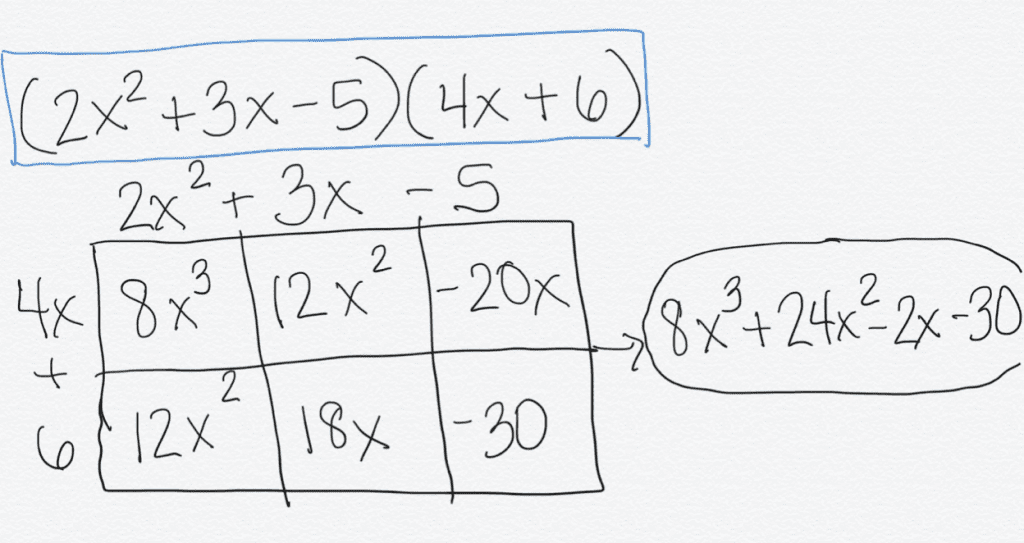
What are the Standards for Mathematical Practice? Why are these important?
The Standards for Mathematical Practice (SMPs) include 8 skills/behaviors that educators work to develop in their math learners. The SMPs are the work that the students do in math class, including making sense of problems. Unlike the content standards, that change from grade to grade, the SMPs remain constant across K-12. Any time children are working on or talking about mathematical ideas, they are using the SMPs. Every math lesson will involve the practice standards, but not every lesson will include each one. While some are more easily observed than others, all of these skills are important in developing a well-rounded mathematician.
 “The mathematical practices for each grade, together with Ohio’s Learning Standards for Mathematics, prescribe that students experience mathematics as a rigorous, coherent, useful and logical subject. The mathematical practices represent a picture of what it looks like for students to understand and do mathematics in the classroom and should be integrated into every mathematics lesson for all students” (Ohio Department of Education).
“The mathematical practices for each grade, together with Ohio’s Learning Standards for Mathematics, prescribe that students experience mathematics as a rigorous, coherent, useful and logical subject. The mathematical practices represent a picture of what it looks like for students to understand and do mathematics in the classroom and should be integrated into every mathematics lesson for all students” (Ohio Department of Education).
Parent Guide about the Standards for Mathematical Practice
*This parent guide includes questions you can ask your child to develop those skills.
What are some ideas to help my child with word problems?
Students will be introduced to a variety of math word problems starting as early as kindergarten. There are many different ways to pose addition, subtraction, multiplication and division problems. They can be 1 step problems or multiple steps.
The question children are asked to solve can differ. Sometimes they are asked for a result – but other times they are asked to find the change or start of a situation. Here are two examples of problems that use the same numbers and context but ask different questions:
| 8 cars were in the parking lot. 2 drove away. How many cars are now in the parking lot? | Some cars were in the parking lot and 2 drove away. Now there are 6. How many cars were in the parking before? |
There can be several reasons why your child may struggle with problem-solving, but hopefully, these suggestions will help ease your worry and raise your child’s confidence in solving word problems. One very common reason why students struggle is they have difficulty understanding the problem.
Reread
Read the problem a couple of times and think about what is being asked. Ask yourself, what information from the problem do I know?
Visualize
When reading a book students need to understand what they are reading and to do that we tell students to make a movie in their mind as they read. We ask students to the same thing when solving word problems. This is called visualization. We want students to visualize rather than look for keywords to help them. Ask your child to provide evidence for what they see in their mind either by acting it out, using manipulatives, and/or drawing a picture.
Take the Numbers Out
Does your child tend to just pull the numbers from the problem and don’t stop and think about what’s being asked? You can remove the numbers and just discuss what is happening in the problem before you attempt to solve it with numbers. This can remove the distractors and take away some anxiety if they are more worried about getting the answer than really understanding the problem.
Act It Out
Let’s say a problem is telling you that someone shares candy. Act out the problem with candy or using a manipulative to represent the candy. This will help students who have trouble making that picture in their mind. After acting it out ask your child to then draw a picture of what they did.
What are some on-line resources to motivate and engage my child?
 ST MATH
ST MATH
Has your child come home and talked about JiJi the penguin? Well, they are talking about ST Math. It’s a visual instructional program that engages students in problem solving and challenges that are developmentally appropriate for their grade level. In each problem, the goal is to get JiJi across the screen because there is something blocking him. By introducing concepts through visual representation it allows students to understand them on a deeper level, compared to other online math games that are skill and drill-based. If you are having trouble setting up your child’s IPad or logging into their account, please contact your child’s teacher or check out the parent resource page on the ST Math website. Another helpful tool on the parent resource page is facilitating questions you can use when your child is stuck on an ST Math Puzzle.
Additional on-line resources
Fluency goes beyond basic facts and is an essential part of computation. For ideas about how students use these strategies, see these brochures from Howard County.


